
Certains cadrans chronographes portent, à côté des divisions habituelles, qui marquent le cinquième de seconde, d’autres graduations servant à un but déterminé ; quelquefois, sur le même cadran, se trouvent plusieurs graduations spéciales, indiquant directement, donc sans calcul, le résultat cherché, à condition que l’observation soit faite d’après une base donnée.
Un cadran portant des divisions spéciales prend le nom de ces divisions ; on dira par exemple : un cadran tachymètre, un cadran pulsomètre, ou même tout simplement : un tachymètre, un pulsomètre, etc.
Le tachymètre (prononcer takimètre), dont le nom, qui vient du grec, est formé de deux racines : takhus, c’est-à-dire rapide, et metron : mesure, est, comme son nom l’indique, gradué en vue de rendre la mesure des vitesses rapide. L’avantage des divisions tachymétrique est, si nous désirons connaître la vitesse à laquelle marche un véhicule, de nous indiquer directement le résultat, nous évitant tout calcul, à condition que l’observation soit faite sur la même distance que celle pour laquelle la graduation a été établie ; cette base d’observation est généralement indiquée sur le cadran.
Le cadran du tachymètre porte une graduation indiquant les vitesses horaires ; c’est-à-dire le nombre de kilomètres à l’heure ; cette graduation se trouve généralement à l’extérieur des divisions marquant les cinquièmes de seconde ; exceptionnellement près du centre du cadran. Les vitesses horaires indiquées par la graduation sont basées généralement sur une distance d’observation de 1000 mètres : quelquefois 200 ou même 100 mètres.
Le tachymètre de la figure 8 porte une graduation basée sur 1000 mètres ; cette base est inscrite sur le cadran, au-dessus de 11 heures.
Le tachymètre s’emploie de la façon suivante: nous désirons connaître la vitesse horaire à laquelle marche une automobile, par exemple ; nous savons que les points A et B placés aux abords de la route sont distants de 1000 mètres. Au moment où l’auto passe devant le point A, nous mettons en marche le chronographe ; lorsqu’elle franchit le point B, nous arrêtons celui-ci et lisons directement, vis-à-vis de la trotteuse, la vitesse horaire ; c’est-à-dire le nombre de kilomètres à l’heure que fait le véhicule.
Admettons, par exemple, que, lorsque nous avons arrêté l’aiguille du chronographe, l’auto franchissant le point B, la trotteuse se trouvait sur la division 30 secondes ; nous lisons, vis-à-vis de la trotteuse, la division tachymétrique 120, nous indiquant que l’auto en question marchait à une vitesse de 120 kilomètres à l’heure ; il est en effet facile de comprendre que, si un véhicule met une demi-minute pour couvrir un kilomètre, il fera 2 kilomètres en une minute et 120 en une heure, soit en 60 minutes. Si cette auto avait mis exactement une minute pour parcourir un kilomètre, elle marcherait à une vitesse de 60 kilomètres à l’heure ; si le temps nécessaire pour couvrir le kilomètre était d’une minute et demie, sa vitesse horaire serait de 40 kilomètre/heure.
Moins le véhicule met de temps pour parcourir une distance donnée (dans le cas présent 1000 mètres) plus sa vitesse est grande.
Si l’on désire savoir (cette question nous a été posée par un fabricant de cadrans) vis-à-vis de quelle division des secondes doit se trouver une division tachymétrique, 90, par exemple, indiquant que si le véhicule a mis ce nombre x de secondes pour parcourir un kilomètre, il fait du 90 à l’heure, on fera le raisonnement suivant :
Puisque le véhicule parcourt 90 kilomètres en une heure, soit en 3600 secondes, il parcourt un kilomètre (base du cadran) en 90 fois moins, soit :
3 x 600 / 90 = 40 secondes.
C’est donc vis-à-vis de la 40ème seconde que se trouvera la division tachymétrique 90, indiquant que, si un véhicule met 40 secondes pour parcourir un kilomètre, il fait du 90 l’heure. Les divisions tachymétriques étant inscrites sur le cadran vis-à-vis des secondes correspondantes, on n’a pas besoin, lors de l’emploi du tachymètre, de s’occuper du temps employé, mais seulement de la distance indiquée comme base, soit généralement 1000 mètres.
Un deuxième exemple : Vis-à-vis de quelle division des secondes doit se trouver la division tachymétrique 45 ?
Appliquons le même raisonnement que précédemment :
Si 45 kilomètres sont parcourus en 3600 sec, 1 kilomètre est parcouru en 45 fois moins
3 x 600 / 45 = 80
Un véhicule qui marche à la vitesse horaire de 45 kilomètres parcourra un kilomètre en 80 secondes ou 1 minute et 20 secondes.
La division tachymétrique 45 se trouvera donc vis-à-vis de la 20ème seconde, mais ne doit être employée que lorsque l’aiguille du compteur de minutes a avancé d’une division depuis le début de l’observation, nous indiquant que ce n’est pas 20 secondes que le véhicule a mis pour parcourir un kilomètre, mais bien 1 minute et 20 secondes.
Pour éviter toute confusion, lors de la lecture. certains cadrans tachymètre portent des divisions de différentes couleurs : c’est ainsi que sur le cadran du tachymètre de la figure 9, la spire extérieure (divisions tachymétriques de 300 à 60) porte des chiffres rouges, de même que la minute zéro du petit cadran de compteur ; on fera donc la lecture sur les graduations de cette spire, lorsque l’aiguille du compteur est restée sur zéro, c’est-à-dire lorsque le temps d’observation n’a pas excédé une minute ; les divisions tachymétriques de la spire suivante, soit de 58 à 30, seront vertes, de même que la minute 1 du compteur ; on fera naturellement la lecture sur les graduations de cette spire, lorsque l’observation a duré plus d’une minute, sans toutefois excéder 2 minutes.
La troisième spire, divisions tachymétriques de 29 à 20, sera jaune, de même que la deuxième minute du compteur et sera employée lorsque l’observation a excédé 2 minutes.

Il existe également des tachymètres basés, non plus sur 1000 mètres, mais sur 200 ou même 100 mètres. Cette base est généralement marquée sur le cadran.
On peut très bien employer un tachymètre basé sur 1000 mètres, pour savoir à quelle vitesse horaire marche un véhicule, en faisant l’observation, non pas sur une distance d’un kilomètre, mais de 200 ou 100 mètres, par exemple ; il suffit de pratiquer tout à fait de la même manière que si l’observation était faite sur 1000 mètres, puis de diviser la vitesse horaire indiquée par l’aiguille, par 5, pour une observation faite sur une distance de 200 mètres, et par 10, pour une observation effectuée sur 100 mètres.
Le pulsomètre est la montre du médecin : ce chronographe possède un cadran dont la graduation indique directement, donc sans calcul, le nombre de pulsations à la minute. La base d’observation est également indiquée sur le cadran; elle est généralement de 30 pulsations: remarquons que ce n’est pas un certain temps qui est observé, mais un nombre donné de pulsations.
L’emploi du pulsomètre est très simple : il suffit, en effet, de mettre en marche le chronographe et de compter le nombre de pulsations indiqué comme base ; naturellement que la pulsation coïncidant avec la mise en marche du chronographe ne doit pas être comptée. A la 30ème pulsation, on arrête le chronographe et l’aiguille trotteuse indique directement, sur la graduation du pulsomètre, le nombre de pulsations à la minute. La figure 10 nous montre un compteur avec cadran pulsomètre.
Pour trouver vis-à-vis de quelle seconde on doit placer, sur le cadran, le chiffre 75, par exemple, nous indiquant que si 30 pulsations, base indiquée sur le cadran, s’accomplissent en ce nombre x de secondes, il y en aura 75 à la minute, on fait le raisonnement suivant :
Si 75 pulsations s’accomplissent en 1 minute, soit en 60 secondes,
1 pulsation s’accomplit en 75 fois moins, 30 pulsations (base du cadran) s’accompliront en 30 fois plus, soit : 60 x 30 / 75 = 24
C’est donc vis-à-vis de la 24ème seconde que se trouvera le chiffre 75, de la graduation du pulsomètre, nous indiquant que si 30 pulsations ont lieu en 24 secondes, il y en aura 75 à la minute.
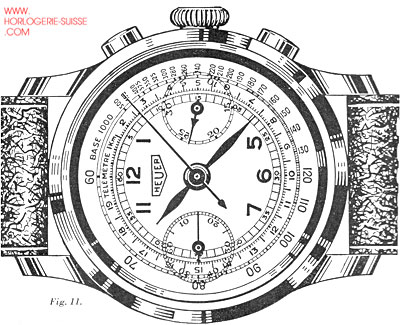
Le télémètre sert à mesurer la distance qui sépare l’observateur d’un phénomène d’abord visible, puis auditif.
La graduation du télémètre est basée sur la vitesse du son dans l’air, qui est de 330,7 mètres à la seconde, soit pratiquement 1 kilomètre en 3 secondes.
Si on désire savoir à quelle distance éclate un orage, par exemple, on met en marche le chronographe au moment où on voit l’éclair ; puis, au moment où on entend le tonnerre, on arrête la trotteuse de celui-ci, l’aiguille indique, sur les divisions télémétriques, la distance séparant l’observateur de l’endroit où le phénomène s’est produit.
Le télémètre était surtout employé en artillerie, pour connaître la distance séparant l’observateur de la batterie ennemie.
Le télémètre que nous venons de décrire ne doit naturellement pas être confondu avec l’appareil du même nom, employé en défense aérienne, par exemple, pour estimer la distance séparant l’avion de la batterie de défense contre avion.
Le chronographe avec cadran dit « de production », figure 12, s’emploie de la façon suivante : si on désire connaître le nombre de pièces qu’un ouvrier ou une machine est capable de produire à l’heure, on met en marche le chronographe, au début de l’opération à effectuer et on arrête la trotteuse lorsque l’opération est terminée ; l’aiguille indique directement, sur la division spéciale, la production à l’heure.
Sur le cadran de la figure 12, on remarque que si le temps nécessaire à exécuter une opération est d’une seconde, par exemple, la production horaire est de 3600 pièces, vu qu’il y a 3600 secondes dans une heure; si, pour exécuter une autre opération, il faut compter 15 secondes par pièce, la production sera de 240 pièces à l’heure.
Si on désire savoir, vis-à-vis de quelle division des secondes il faut placer sur le cadran, un chiffre quelconque de la graduation de production, 100, par exemple, on fera le raisonnement suivant :
Si 100 pièces sont exécutées en 1 heure, soit en 3600 secondes, il faut 100 fois moins de temps pour exécuter une pièce :
soit : 3 x 600 / 100 = 36
C’est donc vis-à-vis de la 36me seconde que doit se trouver le chiffre 100, de la graduation de production.
A côté des cadrans tachymètres, pulsomètres, télémètres et de production, on rencontre des cadrans portant une graduation s’accordant avec la marche de la trotteuse ; c’est ainsi que, dans certains chronographes et compteurs au 1/10 de seconde, l’aiguille exécutant non pas un tour par minute, mais deux, le cadran est divisé en 30 secondes et non pas en 60.
De même, les cadrans de compteurs de sport au 1/50 ou au 1/100 de seconde porteront une division correspondant à la marche de la trotteuse; celle-ci exécutant un tour en 6, respectivement 3 secondes.
Certains cadrans de chronographes et de compteurs de sport portent une graduation s’adaptant à l’épreuve sportive, pour le chronométrage de laquelle ils sont destinés : cadran compteur de 45 minutes pour le football, cadran compteur également, mais portant deux graduations de 7 minutes chacune, pour le water-polo ; etc., etc.
Depuis quelques années, le quantième ou montre calendrier, après avoir été délaissé, a fait sa réapparition ; il complète souvent le chronographe; la figure 13 nous montre un chronographe compteur, avec compteur d’heures et quantième ; le cadran de cette pièce porte deux ouvertures, ou « guichets », permettant de lire, à gauche le jour de la semaine et à droite le nom du mois, les inscriptions, aussi bien des noms des jours de la semaine que de ceux des mois, étant portées par des disques se mouvant sous le cadran ; la date ou quantième du mois est indiquée par une aiguille sur un petit cadran sous midi.
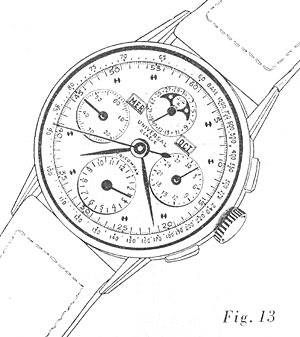
L’utilité du quantième est souvent contestée ; il est certain, cependant, que celui qui a pris l’habitude de consulter sa montre, non seulement pour connaître l’heure, mais également la date, se passe difficilement de ses services.
Sous le nom de « Chronomat » est apparu, depuis quelques années, un chronographe-bracelet portant une petite règle à calcul circulaire ; les divisions spéciales de cette règle à calcul sont indépendantes du chronographe, c’est-à-dire qu’elles n’ont aucun rapport avec la trotteuse de celui-ci.
Le chronomat comporte donc deux appareils réunis en un seul, soit le chronographe avec ses divisions de cadran habituelles et la règle à calcul. La réunion de ces deux appareils est logique, car, comme nous le verrons par quelques exemples, l’observation de temps, donnée par le chronographe, est souvent nécessaire pour résoudre certains problèmes au moyen de la règle à calcul.
L’emploi profitable de toute règle à calcul nécessite un certain entraînement ; il n’en est naturellement pas autrement de celle portée par le chronomat.

La figure 14 nous montre le cadran du chronomat : nous remarquons que celui-ci porte, à l’extérieur des divisions habituelles, une échelle graduée logarithmiquement de 1 à 10, progressant de gauche à droite, donc dans le sens de la marche des aiguilles d’une montre; chaque division porte les subdivisions en dixièmes.
Adjacente au cadran, donc aux divisions de la première échelle, se trouve une deuxième échelle, graduée logarithmiquement de 1 à 10, avec subdivisions en dixièmes également; cette seconde échelle, contrairement à la première, progresse de droite à gauche, donc dans le sens contraire à la marche des aiguilles d’une montre.
La première échelle, portée par le cadran de la montre, est donc fixe, tandis que la seconde est portée par une lunette tournante : on peut donc, en donnant à la lunette un mouvement de rotation, placer un point déterminé de l’une des échelles en regard d’un point quelconque de l’autre.
Les échelles se lisent naturellement dans leur sens de progression, soit de gauche à droite pour l’échelle intérieure, portée par le cadran, et de droite à gauche pour l’échelle extérieure, portée par la lunette tournante : une flèche placée sur l’échelle extérieure indique du reste le sens de progression de celle-ci.
Une remarque importante également : tant que l’espace compris entre deux divisions de l’échelle le permet, le dixième est indiqué après la virgule : exemples : 1,4 1,5 etc : par contre, lorsque les traits des divisions deviennent trop serrés, les traits des subdivisions subsistent, mais le chiffre du dixième est supprimé : il y aura par exemple, entre les chiffres 8 et 9 de l’échelle, 9 traits représentant les dixièmes: la division 8.3 est naturellement la troisième après le 8.
Les échelles ne comportant que des chiffres de 1 à 10 ne semblent permettre que des calculs très restreints : pratiquement, on supprimera mentalement toute décimale en disposant les échelles : par contre, en lisant le résultat, on rétablira la virgule ou on ajoutera le ou les zéros éventuellement nécessaires ; en réalité, la chose est plus simple qu’elle ne le paraît ; car, lors d’un calcul de vitesse horaire, par exemple, si l’on obtient comme résultat 6,6, on comprendra immédiatement que celui-ci est juste et que, par conséquent, il n’est pas à modifier s’il s’agit de la vitesse horaire d’un marcheur que, par contre, c’est 66 kilomètres à l’heure qu’il faut lire s’il s’agit d’une automobile et 660, si la vitesse horaire contrôlée est celle d’un avion.
Comme les calculs dans lesquels entre le facteur « temps », problèmes tachymétriques, par exemple, se font aussi bien en réduisant ce temps en 1/5 de seconde, en secondes, en minutes ou en heures, mais que, par contre, le résultat doit être obtenu en vitesse horaire, soit en kilomètres par heure, on trouve sur l’échelle intérieure quatre repères de couleur, dont nous verrons l’utilité plus loin ; le premier de ces repères est marqué H, soit heure, il se trouve vis-à-vis de l’unité (chiffre 1 de l’échelle intérieure), puis, un deuxième repère marqué minutes se trouve vis-à-vis du chiffre 6, vu qu’il y a 60 minutes dans une heure ; le troisième est marqué S, soit secondes ; il est placé vis-à-vis de 3,6, car il y a 3600 secondes dans une heure; enfin, le repère 1/5 se trouve vis-à-vis de 1,8, vu qu’il y a 18 000 cinquièmes de secondes dans une heure.
Prenons quelques exemples de calculs tachymétriques ; nous avons vu qu’il existe des cadrans tachymétriques, nous donnant directement la vitesse horaire, la graduation de ceux-ci étant préparée d’après une certaine distance choisie comme base (généralement 1 kilomètre). Avec le chronomat, le calcul tachymétrique est un peu moins simple qu’avec le tachymètre, mais le chronomat offre l’avantage de pouvoir calculer la vitesse horaire sur n’importe quelle distance et non plus sur une distance choisie une fois pour toute comme base.
Pour tout calcul tachymétrique, la règle suivante est à observer : porter le chiffre représentant la longueur du parcours contrôlé (échelle extérieure) en regard du point de repère (échelle intérieure) de l’unité de temps choisie pour les calculs ; soit repère 1/5, si le temps est exprimé en 1/5 de seconde ; repère S, si celui-ci est en secondes ; repère « Minutes », s’il est indiqué en minutes et repère H, c’est-à-dire heure, si le temps est donné en heures.

Prenons le problème le plus simple.
Un automobiliste a parcouru un kilomètre en 40 secondes. Quelle est sa vitesse horaire ?
Placer le 1 (1 kilomètre, longueur du parcours contrôlé), de l’échelle extérieure, en face du repère S (puisque le temps est exprimé en secondes), position indiquée par la petite flèche de la figure 15 nous chercherons ensuite quel chiffre coïncide avec 4 (40 secondes, durée du parcours), nous voyons que c’est le 9 (figure 15, flèche plus épaisse). Ce n’est naturellement pas 9 kilomètres à l’heure que fait l’auto, mais bien du 90.
On peut poser le problème de la manière inverse ; soit : un automobiliste a roulé durant 40 secondes, à la vitesse horaire de 90 kilomètres. Quelle distance a-t-il couverte? Faire alors coïncider 9 (90 kilomètres à l’heure) avec 4 (40 secondes) et lire, vis-à-vis du repère S (puisque le temps est exprimé en secondes), le trajet couvert, soit 1 kilomètre.
A titre d’exemple, voici un deuxième problème tachymétrique :
Un sauteur à skis effectue un saut de 55 mètres de long en 3 secondes et 2/5 ; quelle est sa vitesse horaire ?
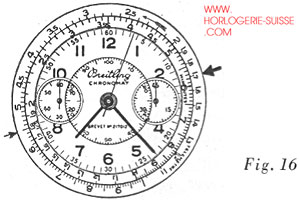
Placer 5,5 (55 mètres, longueur du saut), de l’échelle extérieure, en face du repère 1/5 (figure 16, petite flèche), vu que le temps est exprimé en 1/5. Comme 3 secondes et 2/5 = 17 cinquièmes de secondes, lire, face au chiffre 1,7 de l’échelle extérieure, le chiffre coïncidant de l’échelle intérieure, soit 5,8 (voir figure 16, flèche plus épaisse). La vitesse horaire est de 58 kilomètres à l’heure.
Lors de courses sur piste, si on désire connaître la vitesse horaire des concurrents, à chaque tour de piste, on place, une fois pour toutes, le chiffre représentant la longueur de la piste, en face de l’unité de temps choisie pour les observations.
On lira alors, sur l’échelle, la vitesse horaire des concurrents, à chaque tour de piste, en face du chiffre représentant le temps mis pour accomplir ce tour de piste.
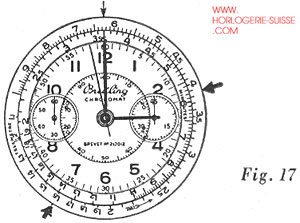
Admettons que la longueur de la piste soit de 6 kilomètres 250 mètres et que le temps soit chronométré en secondes ; on place 6,25 de l’échelle extérieure vis-à-vis du repère S (voir figure 17, petite flèche).
Si le tour de piste était effectué en 58 secondes, on lirait immédiatement, face à 5,8 de l’une des échelles, l’intérieure, par exemple, le chiffre correspondant de l’autre échelle et qui est la vitesse horaire, soit 3,88 (le dernier chiffre se lisant au jugé) (voir figure 17, flèche épaisse à droite). La vitesse horaire serait donc de 388 kilomètres à l’heure.
Si le temps pour effectuer le même tour de piste est de 2 minutes 40 secondes, par exemple, on lit, vis-à-vis de 1,6 (160 secondes) le chiffre représentant la vitesse horaire, soit 1,4 ; c’est-à-dire 140 kilomètres à l’heure (le calcul donne exactement une vitesse horaire de 140 kilomètres 625 mètres).
Pour les calculs télémétriques, il existe sur l’échelle extérieure un repère marqué « Télémètre » ; il se trouve sur le chiffre 1,2 de cette échelle, le son parcourant dans l’air 1200 kilomètres à l’heure.
Lors de problèmes télémétriques, placer le repère « Télémètre » en face du chiffre représentant le temps chronométré, puis, lire, vis-à-vis du repère de l’unité de temps employée (généralement pour les calculs télémétriques, le repère S, secondes), la distance parcourue par le son.
Si l’on désire savoir à quelle distance éclate un orage : au moment où l’on voit un éclair, on met en marche le chronographe; puis, on arrête la trotteuse de celui-ci lorsqu’on entend le tonnerre ; on chronomètre donc le temps séparant l’éclair du coup de tonnerre.
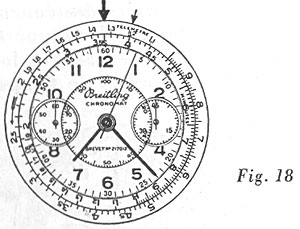
Admettons que le temps entre l’éclair et le tonnerre soit de 4 secondes. Placer le repère « Télémètre » vis-à-vis de 4 (temps observé) (figure 18, petite flèche) ; puis, lire face au repère S (unité de temps employée) le chiffre correspondant à la distance parcourue par le son ; soit 1,33 (le dernier chiffre se lit au jugé) (voir figure 18, flèche plus épaisse). L’observateur se trouve à 1 kilomètre 330 mètres du phénomène.

Pour le calcul du nombre de pulsations à la minute, placer le chiffre représentant les pulsations comptées vis-à-vis du repère « Minutes », et lire, face au nombre de secondes totalisant la durée de l’observation, le nombre de pulsations à la minute.
Exemple : On a compté 27 pulsations en 24 secondes ; combien y en a-t-il à la minute ?
Placer 2,7 (27, nombre de pulsations) en face du repère « Minutes » (figure 19, petite flèche); puis lire, face à 2,4 (24 secondes, temps d’observation), le chiffre correspondant au nombre de pulsations à la minute, soit 6,7, c’est-à-dire 67 pulsations à la minute (voir figure 19, flèche plus épaisse). Le calcul donne exactement 67,5 pulsations à la minute.
Lors de calculs de production, amener le chiffre 1 de la règle extérieure face au repère S, si le chronométrage est effectué en secondes, ou face au repère « Minutes » s’il est en minutes ; lire ensuite, face au chiffre représentant le nombre de secondes (respectivement de minutes, si le chronométrage est effectué en minutes) nécessaires à l’exécution d’une pièce, la production possible à l’heure.
Exemple : Une machine produit une pièce en 4 secondes ; quelle est sa production à l’heure ?
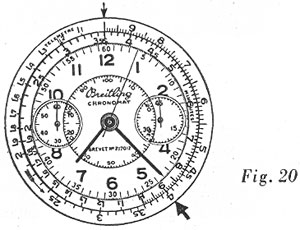
Placer le chiffre 1 (règle extérieure) vis-à-vis du repère S (le temps étant chronométré en secondes) ; lire en face de 4 (4 secondes, temps nécessaire à la production d’une pièce) la production possible à l’heure, soit 900 (voir figure 20).
Naturellement que le chronomat peut être employé comme « règle à calculs », lors de problèmes pour lesquels le facteur « temps » n’entre pas en ligne de compte ; son emploi, comme nous l’avons déjà dit, nécessite un certain entraînement ; il est forcément limité à des problèmes ne comportant pas de trop grands nombres.
Pour opérer une multiplication, par exemple, il suffit de faire coïncider multiplicande et multiplicateur ; en regard du 1 de l’une ou de l’autre des échelles, on lira le résultat.
Exemple : 3 x 18 ? Faire coïncider 3 de l’une des échelles avec 1,8 de l’autre et lire, vis-à-vis du 1 de l’une des échelles, le résultat soit 54 (voir figure 21).

Pour la division, on procède de façon inverse; c’est-à-dire que l’on amène le 1, de l’une ou l’autre des échelles, en regard du dividende ; on crée ainsi toute une table de division de ce nombre, le résultat se lisant face au diviseur.
Exemple : Pour diviser 54, on place le 1 de l’une des échelles face à 5,4 ; si c’est par 18 que l’on désire diviser 54, on lit le résultat vis-à-vis de 1,8, soit 3 ; si on veut diviser 54 non plus par 18, mais par 45, on lit le résultat face à 4,5, soit 1,2 (figure 21).
La règle de trois étant une multiplication, puis une division du résultat de cette multiplication par un diviseur, elle s’effectue, grâce aux échelles logarithmiques, en une seule opération, ce qui se conçoit aisément puisque le résultat de la multiplication se lit face à 1, de l’une ou l’autre des échelles, et que ce résultat devient, lors de la division, le dividende, à placer également en face du 1 de l’une ou l’autre des échelles ; il suffit donc, pour opérer une règle de trois, de faire coïncider multiplicande et multiplicateur, puis de lire, face au diviseur, le résultat.
Exemple : 3X18 /12
Pour opérer cette règle de trois, faire coïncider 3 et 1,8, puis lire vis-à-vis de 1,2 le résultat, soit : 4,5.
La règle de trois est donc très simple à effectuer.
Le chronomat permet de résoudre bien des problèmes ; il ne remplacera cependant certes pas une bonne règle à calcul, ne pouvant, vu sa dimension, porter toutes les graduations de celle-ci.
A notre connaissance, bien des jeunes gens apprécient le chronomat ; en s’habituant à l’employer pour des calculs simples, ils se familiarisent avec l’emploi des échelles logarithmiques.

La figure 22 représente un appareil de haute précision, dont le cadran porte des graduations toutes spéciales ; c’est le « Sidérographe ».
M. Fréd.-E. Pfister, ingénieur à la Compagnie des montres « Longines », dans une très intéressante étude intitulée : « Navigation aérienne et chronométrie », publiée dans la Dépêche de l’Air, donne la description complète du sidérographe. C’est de cette étude que sont tirées les quelques explications indispensables à la connaissance des graduations du sidérographe.
La navigation aérienne au long cours utilise, à côté de différentes méthodes, celle dite de « navigation astronomique ». Vu la vitesse très grande de l’avion, les moyens dont dispose la navigation maritime ne sont plus suffisamment rapides, pour déterminer sa position ; il a donc été nécessaire de construire des appareils permettant de « faire le point » avec une très grande rapidité.
Le sidérographe a été créé dans ce but ; ici encore, c’est par des graduations appropriées, supprimant, dans la mesure du possible, les calculs, que le problème a été résolu ; problème qui consistait à construire un appareil permettant de déterminer rapidement les a angles horaires » des étoiles, par rapport au méridien de Greenwich ; détermination indispensable pour les vols de nuit.
Par suite, du développement croissant de l’aviation au long cours, les instituts nautiques de divers pays ont transformé toutes les coordonnées, nécessaires au calcul de position, en valeur angulaire ; ce fait, de même que celui, nouveau également, de pouvoir considérer tous les astres dans leur mouvement sidéral, permit l’emploi d’une montre angles horaires, réglée au temps sidéral.
Le sidérographe, comme son nom l’indique, est donc une montre réglée au temps sidéral, ses aiguilles avançant au rythme du mouvement apparent diurne des étoiles ; il permet de fixer le a sidéral » nécessaire pour la détermination de l’angle horaire.
Venons-en aux graduations du cadran : la graduation moyenne de celui-ci est divisée, tous les 10 degrés, de 0 à 360 degrés ; elle est lue par une aiguille effectuant un tour en 24 heures sidérales. La graduation intérieure de 1 à 10 degrés marque les unités ; elle est lue par une aiguille faisant un tour en 40 minutes sidérales. La graduation extérieure est divisée en 60 minutes d’arc, chaque minute étant divisée elle-même en 5 parties, ce qui permet d’apprécier le 110 de minute d’arc. Les minutes d’arc sont donc lues, sur cette graduation, au moyen de l’aiguille trotteuse ou des aiguilles de rattrapante, qui exécutent un tour en 4 minutes sidérales. Alors que la trotteuse possède un mouvement continu, permettant de connaître constamment la marche du sidérographe, on peut arrêter successivement l’une, puis l’autre des aiguilles de rattrapante ; puis, la lecture étant effectuée, les ramener toutes deux sur la trotteuse.
Le cadran des minutes d’arc, portant les graduations de 0 à 60, est un cadran tournant, ce qui permet la remise à la seconde sans influencer la marche de la montre ; la remise à la seconde s’effectue de la façon suivante : au signal horaire, on arrête une des aiguilles de rattrapante ; puis, en faisant tourner le cadran, on. amène le 60 de celui-ci, sous l’aiguille de rattrapante ; de cette façon, la remise à la seconde est effectuée sans toucher au mouvement.
Les deux aiguilles de rattrapante permettent de faire des observations précises à n’importe quel moment ; elles sont employées pour fixer le sidéral. L’emploi du sidérographe est inséparable de celui du sextant ; or, les sextants employés en aviation utilisent un horizon artificiel constitué par un niveau à bulle d’air. La vitesse de l’avion imprime à la bulle d’air des accélérations nuisibles à la précision des observations ; c’est pourquoi, clans un intervalle de 3 minutes, on relève 6 hauteurs consécutives de l’astre, dont on prend la moyenne, la première aiguille de rattrapante étant arrêtée lors de la première observation, et la seconde aiguille de rattrapante, lors de la 6ème ; le sidéral moyen, correspondant à la hauteur moyenne, est représenté par la bissectrice de l’angle formé par les deux aiguilles de rattrapante.
Un dispositif électrique permet la commande à distance des aiguilles de rattrapante. Le cadran peut être éclairé électriquement. Un dispositif de chauffage, électrique lui aussi, commandé par un thermostat de réglage, empêche la température de descendre en dessous de +20 degrés centigrade. Au cadran du sidérographe est adjointe une lunette loxodromique permettant quelques déterminations à l’estime, auxiliaire précieux pour le navigateur aérien. Les grandes graduations de la lunette représentent
les angles de 0 à 90 degrés. Les chiffres extérieurs donnent les cosinus des angles indiqués, multipliés par 100, pour faciliter les calculs. Les chiffres intérieurs sont destinés à trouver rapidement les sinus et les cosinus des angles sous-multiples de 5 degrés.
Comme nous pouvons le constater, la chronométrie a joué un rôle important dans le domaine de la navigation aérienne, ce qui est tout à son honneur.
Nous voilà loin du télémètre…
Nous avons estimé utile d’étudier, d’une façon approfondie, les graduations que l’on rencontre sur les cadrans de chronographes, car, à plusieurs reprises, nous avons reçu des demandes de renseignements concernant celles-ci.


